Man and History: 1月 2023

2023年1月29日星期日

朱倍贤教授原始佛法32讲

2022/12/17

-----

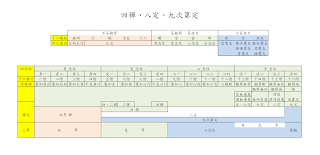
圖一、四禪、八定、九次第定 [6]。

-----

# 2023/01/29

# 32

# 五蘊

https://www.youtube.com/watch?v=KeZMzgqAoGM

# 2023/01/28

# 31

# 全身呼吸

https://www.youtube.com/watch?v=7g9mvFmDMOc

# 2023/01/27

# 30

# 五禪支

https://www.youtube.com/watch?v=lZTDHTGLaPE

# 2023/01/26

# 29

# 掉悔

https://www.youtube.com/watch?v=v7Panv_eSTE

# 2023/01/25

# 28

# 離生喜樂

https://www.youtube.com/watch?v=HwhtEvoIymc

# 2023/01/24

# 27

# 沒有聽出特別的重點

https://www.youtube.com/watch?v=ZBYFsWx4gMo

# 2023/01/23

# 26

# 體驗樂

https://www.youtube.com/watch?v=nu57swtncOY

# 2023/01/22

# 25

# 初果

https://www.youtube.com/watch?v=G-oaFrRqSvo

# 2023/01/21

# 24

# 佛教歷史簡述

https://www.youtube.com/watch?v=3AilZov7h98

# 2023/01/20

# 23

# 初果其中之一為斷戒禁取

https://www.youtube.com/watch?v=RNdqnwflyPg

# 2023/01/19

# 22

# 初果斷我見二果減我愛三果斷我愛四果斷我慢

https://www.youtube.com/watch?v=OfNRJZupiOc

# 2023/01/18

# 21

# 出離心

https://www.youtube.com/watch?v=SnfbZrT5Yxg

# 2023/01/17

# 20

# 身念住身內身受念住法念住遠離

https://www.youtube.com/watch?v=9nh_6ViIhpQ

# 2023/01/16

# 19

# 法念住

https://www.youtube.com/watch?v=EQf1rEIi8ng

# 2023/01/15

# 18

# 心念住慈捨

https://www.youtube.com/watch?v=vMmGbzQrebY

# 2023/01/14

# 17

# 心念住

https://www.youtube.com/watch?v=jB5ENFWrKt8

# 2013/01/13

# 16

# 身中身自主神經受念住

https://www.youtube.com/watch?v=Lp4DwDc3eh8

# 2023/01/11

# 15

# 四大

https://www.youtube.com/watch?v=8TkzDKTOcio

# 2023/01/10

# 14

# 呼吸時覺知全身

https://www.youtube.com/watch?v=fx_LO9iyR3I

# 2023/01/09

# 13

# 瞭解心架構心釋放心

https://www.youtube.com/watch?v=EYGWU_wWxN0

2023/01/07

# 12

# 八風平捨內外的緩衝身念住四正勤

https://www.youtube.com/watch?v=e7b70xp4Sx4

2023/01/06

# 11

# 四念住

https://www.youtube.com/watch?v=9SpZdkpFz7U

2023/01/05

# 10

# 四念住（身念住：觀察呼吸、姿勢。受念住：觀察動機，心念住：觀察念頭）

https://www.youtube.com/watch?v=mr01OPJO9cU

2022/12/31

# 09

# 初禪。之後每階都停留一段時間，熟練後捨離，再進入下一階。

https://www.youtube.com/watch?v=BQ6w70d4Wms

2022/12/30

# 08

# 慈心、令心歡喜（慈悲喜捨可交替運用）

https://www.youtube.com/watch?v=9OJGcabMkuY

2022/12/29

# 07

# 身念住（周圍神經）、受念住（自主神經）、心念住（中樞神經）

https://www.youtube.com/watch?v=cvirtgyjVKE&t=53s

2022/12/28

# 06

# 戲論、戒禁取

https://www.youtube.com/watch?v=eFYYv8f1aNg

2022/12/23

# 05 食厭想

https://www.youtube.com/watch?v=1bSIRgrBTr8

2022/12/22

# 04

# 食

https://www.youtube.com/watch?v=-xLyA5RCUqA

2022/12/21

# 03

# 集滅味患離

# 打坐時腰椎稍微用一點點力往前挺

https://www.youtube.com/watch?v=XMbgyeuP5s0

2022/12/18

# 02

# 有（becoming）

https://www.youtube.com/watch?v=WIh6DLqlbx4

2022/12/17

# 01

https://www.youtube.com/watch?v=QcCi05S71rs

-----

References

[1] 朱倍賢簡介 | 4ariyasacca

https://wgf9966.wixsite.com/4ariyasacca/blank-mzekn

[2] Religious Studies – Graduate Program | University of the West

https://www.uwest.edu/religious-studies-graduate-program/

[3] William Chu

https://www.international.ucla.edu/buddhist/person/1003

[4] A Buddha-shaped Hole: Yinshun's (1906-2005) Critical Buddhology and the Theological Crisis in Modern Chinese Buddhism

http://buddhism.lib.ntu.edu.tw/en/search/search_detail.jsp?seq=147864

[5] Bodhisattva Precepts in the Ming Society: Factors behind their Success and Propagation

https://buddhism.lib.ntu.edu.tw/en/search/search_detail.jsp?seq=133469&comefrom=authorinfo

[6] 定

http://mandhistory.blogspot.com/2022/10/samadhi.html

-----

林居禪園筆記

http://mandhistory.blogspot.com/2022/01/blog-post_22.html

-----

2023年1月17日星期二

Python 量子運算（C）：安裝元件

2023/01/17

-----

https://pixabay.com/zh/photos/censorship-limitations-610101/

-----

代碼一

1 2	!pip install qiskit !pip install qiskit[visualization]

解說：

安裝 Qiskit [1]。參考 [5]。

-----

代碼二

1
2
3

!pip install pycodestyle pycodestyle_magic
!pip install flake8
%load_ext pycodestyle_magic

解說：

維持良好的 coding style [2]。參考 [5]。

-----

代碼三

1
2
3

from google.colab import drive
drive.mount('/content/drive/')
!ls '/content/drive/My Drive/'

解說：

使用 Google drive [3]。參考 [6]。

-----

代碼四

!sudo apt-get update
!sudo apt-get install texlive-latex-recommended 
!sudo apt-get install dvipng texlive-latex-extra texlive-fonts-recommended  
!wget http://mirrors.ctan.org/macros/latex/contrib/type1cm.zip 
!unzip type1cm.zip -d /tmp/type1cm 
!cd /tmp/type1cm/type1cm/ && sudo latex type1cm.ins
!sudo mkdir /usr/share/texmf/tex/latex/type1cm 
!sudo cp /tmp/type1cm/type1cm/type1cm.sty /usr/share/texmf/tex/latex/type1cm 
!sudo texhash 
!apt install cm-super

解說：

在 Colab 上使用 LaTex [4]。參考 [7]。

-----

References

# Qiskit

[1] 輕鬆學量子程式設計

https://staff.csie.ncu.edu.tw/jrjiang/qbook/

# Colab Pylint

[2] Is there a python style checker that works on notebooks in google colab? - Stack Overflow

https://stackoverflow.com/questions/62154714/is-there-a-python-style-checker-that-works-on-notebooks-in-google-colab

# Colab

[3] 玩具烏托邦: 貴哥的 colab 初學筆記

https://newtoypia.blogspot.com/2019/07/colab.html

# Colab LaTex

[4] (29) Make Latex Work with Matplotlib on Google Colab - YouTube

https://www.youtube.com/watch?v=yySQ-6mh8yo

[5] Python 量子運算（一）：量子電路

http://mandhistory.blogspot.com/2022/11/blog-post_16.html

[6] Python 量子運算（二）：量子位元符號

https://mandhistory.blogspot.com/2022/11/blog-post_3.html

[7] Python 量子運算（三）：量子位元基底

https://mandhistory.blogspot.com/2022/11/blog-post_22.html

-----

Python 量子運算（目錄）

https://mandhistory.blogspot.com/2022/01/quantum-computing.html

-----

Python 量子運算（B）：精華資料

2022/12/01

-----

量子運算精華資料：

1. Wave - 演算法筆記 # DFT（秀爾演算法的基礎）

2. 量子電腦設計原理

3. 書籤分享 | A blue-sky wanderer

4. QRunes # 量子運算演算法中文簡介

5. Jehn-Ruey Jiang # 簡明的實作

6. Qiskit # 詳細的實作

7. Quantum Computation and Quantum information # 量子運算的理論準備

8. Cirq # 進階的實作

-----

量子運算基本資料：

# 量子運算中文書

# 量子運算影片精選

# Quantum Computing News

-----

目標：掌握基本的數學原理，實作演算法，是這一系列文章的目的。

權利：獲得進入量子運算世界的基本技能。

義務：花時間讀，花時間想，與花時間做。網路版為免費，紙本書請期待。

-----

https://pixabay.com/zh/photos/censorship-limitations-610101/

-----

Python 量子運算（目錄）

https://mandhistory.blogspot.com/2022/01/quantum-computing.html

-----

2023年1月9日星期一

四取

Upādāna

2022/10/17

-----

圖一、心如熾火。

-----

「「四取」：欲取（執著欲貪）、見取（執著邪見）、戒禁取（執著與解脫無關的禁戒或禁忌）、我與取（執著「有我」的言論）。」[2]。

「凡夫的心有欲取、見取、戒取、我語取等四取，故心如熾火，煩惱痛苦。智者的心放下四取，故心如釋火，解脫自在。佛法大量利用火的意象，說明人生境況，既貼切又生動，佛可謂擅喻者也。」[4]。

-----

References

[1] 取 (佛教) - 維基百科，自由的百科全書

https://zh.wikipedia.org/wiki/%E5%8F%96_(%E4%BD%9B%E6%95%99)

[2] agama:四受 - 台大獅子吼佛學專站

http://buddhaspace.org/main/modules/dokuwiki/agama:%E5%9B%9B%E5%8F%97

[3] 香光莊嚴第八十四期/專欄/春風化雨/四取

http://www.gaya.org.tw/magazine/v1/2005/84/84c1.htm

[4] gaya/佛教圖書館館訊/第三十八期/《心如熾火》導讀

http://www.gaya.org.tw/journal/m38/38-book2.htm

[5] 心如熾火

https://webpacx.ksml.edu.tw/bookDetail/680121

[6] 非我 – 原始佛法～林居禪園

https://4ariyasacc2.wordpress.com/2016/10/31/%E9%9D%9E%E6%88%91%E4%B8%8B/

[7] 色界禪 – 原始佛法～林居禪園

https://4ariyasacc2.wordpress.com/2015/10/31/%E8%89%B2%E7%95%8C%E7%A6%AA/

[8] 厭離心 – 原始佛法～林居禪園

https://4ariyasacc2.wordpress.com/2015/10/31/%E5%8E%AD-%E9%9B%A2-%E5%BF%83/

[9] 離欲尋 – 原始佛法～林居禪園

https://4ariyasacc2.wordpress.com/2016/05/30/%E9%9B%A2%E6%AC%B2%E5%B0%8B/

[10] 簡述「我慢」 – 原始佛法～林居禪園

https://4ariyasacc2.wordpress.com/2016/03/02/%E7%B0%A1%E8%BF%B0%E3%80%8C%E6%88%91%E6%85%A2%E3%80%8D/

[11] 平捨心—出世間法的橋樑 – 原始佛法～林居禪園

https://4ariyasacc2.wordpress.com/2014/08/01/%E5%B9%B3%E6%8D%A8%E5%BF%83-%E5%87%BA%E4%B8%96%E9%96%93%E6%B3%95%E7%9A%84%E6%A9%8B%E6%A8%91/

遠離

厭離

離欲

滅

捨

-----

林居禪園筆記

http://mandhistory.blogspot.com/2022/01/blog-post_22.html

-----

2023年1月2日星期一

Python 量子運算（一三）：狄拉克標記

2022/12/07

-----

Fig. 13.1. Dirac notation (p. 62) [1].

-----

代碼 13.1

# Program 13.1：Dirac notation
import matplotlib as mpl
import matplotlib.pyplot as plt

# figure setting
mpl.rcParams['text.usetex'] = True
mpl.rcParams['text.latex.preamble'] = r'\usepackage{{amsmath}}'
mpl.rcParams['font.size'] = 40
fig, ax = plt.subplots(figsize=(16, 16))

# Notation
nttn = ['Notation',
        r'$z^*$',
        r'$\vert\psi\rangle$',
        r'$\langle\psi\vert$',
        r'$\langle\phi\vert\psi\rangle$',
        r'$\vert\phi\rangle\bigotimes\vert\psi\rangle$',
        r'$\vert\phi\rangle\vert\psi\rangle$',
        r'$A^*$',
        r'$A^T$',
        r'$A^\dag$',
        r'$\langle\phi\vert A\vert\psi\rangle$'
        ]

# Description
dctn = ['Description',
        r'${\rm Complex\ conjugate\ of\ the\ complex\ number}\ z.$',  # 1
        r'${\rm Vector.\ Also\ known\ as\ a\ }ket.$',                 # 2
        r'${\rm Vector\ dual\ to\ \vert\psi\rangle.'                  # 3
        r'\ Also\ known\ as\ a\ }bra.$',                              # 3
        r'${\rm Inner\ product\ between\ '                            # 4
        r'\vert\phi\rangle\ and\ \vert\psi\rangle.}$',                # 4
        r'${\rm Tensor\ product\ of\ '                                # 5
        r'\vert\phi\rangle\ and\ \vert\psi\rangle.}$',                # 5
        r'${\rm Tensor\ product\ of\ '                                # 6
        r'\vert\phi\rangle\ and\ \vert\psi\rangle.}$',                # 6
        r'${\rm Complex\ conjugate\ of\ the\ }A\ {\rm matrix}.$',     # 7
        r'${\rm Transpose\ of\ the\ }A\ {\rm matrix}.$',              # 8
        r'${\rm Hermitian\ conjugate\ or\ adjoint,\ }$'               # 9
        r'$A^\dag=(A^T)^*.$',                                         # 9
        r'${\rm Inner\ product\ between\ '                            # 10
        r'\vert\phi\rangle\ and\ }A\vert\psi\rangle.$']               # 10

for i in range(11):
    ax.text(0.05, 1-0.1*i, nttn[i])
    ax.text(0.25, 1-0.1*i, dctn[i])

ax.set_axis_off()

# plt.savefig('/content/drive/My Drive/pqc/0013_001.png')
plt.show()

解說：

-----

References

[1] Quantum Computation and Quantum Information

https://www.amazon.com/Quantum-Computation-Information-10th-Anniversary/dp/1107002176

[2] Dirac notation - Azure Quantum | Microsoft Learn

https://learn.microsoft.com/en-us/azure/quantum/concepts-dirac-notation

[3] 量子世界的基本數學 - 白話文量子演算法

https://chiwei955201314.gitbook.io/quantum/

-----

Python 量子運算（目錄）

https://mandhistory.blogspot.com/2022/01/quantum-computing.html

-----

2023年1月1日星期日

Quantum Note

2022/11/15

-----

https://pixabay.com/zh/photos/notepad-table-decoration-notes-3297994/

-----

2023/01/01

# 量子演算法

Deutsch-Jozsa

預言：輸入一個 n 位元的二進位字串並輸出一個位元，該位元是將函式 f 應用於二進位字串的結果。我們承諾函式 f 是常數（在這種情況下，總是輸出一樣的位元），或者是平衡的（在這種情況下，輸出 0 和 1 的次數是相同的）。

問題：以最少的 oracle 查詢次數，完全確定 f 是常數還是平衡的。

查詢複雜度：傳統上，我們需要對 oracle 進行 2^(n-1)+1 次查詢，以完全確定函式的性質。若使用 QPU，則用一次量子查詢即可以零錯誤的機率解決這個問題！

Bernstein-Vazirani

預言：輸入一個 n 位元的二進位字串 x，並輸出一個二進位數字。該輸出是由計算 Σi xi‧si 而來，其中 s 是 oracle 所使用的一個秘密字串。

問題：找到秘密字串 s。

查詢複雜度：傳統上，我們需要執行 n 次 oracle 查詢，每次查詢需要瞭解一個輸入位元。然而，使用 QPU 只需查詢一次即可解決這個問題。

Simon

預言：輸入一個 n 位元的二進位字串 x，並輸出一個整數。所有可能的輸入字串都透過秘密字串 s 來配對，如此一來，兩個字串 (x, y) 會產生相同的輸出，若且唯若 y = x ⊕ s（其中 ⊕ 表示模數 2 的位元加法）。

問題：找到秘密字串 s。

查詢複雜度：傳統的確定性演算法至少需要 2^(n-1)+1 次 oracle 查詢，而使用 Simon 量子演算法，可以用線性的 n 次呼叫 oracle 找到答案，而非指數級次數的呼叫。

量子電腦程式設計 : 演算法精要與程式範例

http://books.gotop.com.tw/v_A605

-----

2022/12/06

# 引號

究竟在什麼時候應該加上引號，什麼時候不加呀？ -CSDN社區

https://bbs.csdn.net/topics/30294691

-----

2022/11/26

# Superposition

particle physics - 是否已實際證明存在量子疊加？如果是，它是如何工作的？ - 物理堆棧交換

https://physics.stackexchange.com/questions/582737/has-it-been-practically-proven-that-quantum-superposition-exists-if-yes-how-d

# Superposition

Superposition, Reversibility and the Entanglement Frontier

https://www.qmunity.tech/post/superposition-reversibility-and-the-entanglement-frontier

-----

2022/11/22

# Quantum Machine Learning

Awesome Quantum Machine Learning | awesome-quantum-machine-learning

https://krishnakumarsekar.github.io/awesome-quantum-machine-learning/

# Bloch sphere

Plotting on the Bloch Sphere — QuTiP 3.1.0 Documentation

https://qutip.org/docs/3.1.0/guide/guide-bloch.html

# Bloch sphere

Python QuTiP Saving Bloch sphere as .png and .pdf - Stack Overflow

https://stackoverflow.com/questions/24666216/python-qutip-saving-bloch-sphere-as-png-and-pdf

# Bloch sphere

python 3.x - The length of an arrow in the Bloch sphere - Stack Overflow

https://stackoverflow.com/questions/53203197/the-length-of-an-arrow-in-the-bloch-sphere

# Bloch sphere

python - Good-looking sphere in Matplotlib - Stack Overflow

https://stackoverflow.com/questions/70443422/good-looking-sphere-in-matplotlib

# LaTeX

math mode - Braket notation in LaTeX - TeX - LaTeX Stack Exchange

https://tex.stackexchange.com/questions/214728/braket-notation-in-latex

# Dirac

Day 1: Dirac Notation and Operators

https://deepnote.com/@QC-Workshop-Summer-2021/Day-1-Dirac-Notation-and-Operators-bd5299ba-3552-4245-ace3-7520a3ce29d1

-----

2022/11/15

# zero capacity

「A fundamental prediction of the capacity formula is that the only channels with zero capacity are precisely those for which the input and output are completely uncorrelated.」

https://arxiv.org/abs/0807.4935

-----

Bloch or Q-Sphere

2022/05/16

「from numpy import sqrt

from qiskit.visualization import plot_bloch_multivector

plot_bloch_multivector([1/sqrt(2), 1/sqrt(2)])」

https://github.com/Qiskit/qiskit-terra/issues/4770

-----

qiskit

2022/05/16

「pip install qiskit」